|
|
|
![]()

Maya Calendrical Geometry. (04/05/2001)
Part I: To construct an equilateral triangle on any given finite straight line cut in extreme/ mean ratio.
A first problem that must be solved in the creation of a Euclidean
geometry is the construction of an equilateral triangle. Once
that task is successfully accomplished, every other figure and
proof in The Elements can be achieved. That the Maya were
probably able to conceptualize an equilateral triangular space
during the Classic period using only a compass and a straight-edge,
and do so in a fashion that was uniquely their own without recourse
to Euclid's actual methodology, can be inferred from the fact
that such a construction and proof is preeminently possible, if
not simplistically attainable, using the precise geometrical limitations
and paradigms already in place in the figure identified elsewhere
(Maya Calendrical Harmonics)
as a geometrical expression of the 260-day Tzolkin. In
fact, to accomplish the goal of constructing the equilateral triangle
on that figure, it is necessary to add but a single straight line
to the elements already in place. This is true, and demonstrable,
because any straight line which connects two 18 degree angle intersections
with the outer circle (whose radius is equal to the extreme segment
of the extreme/ mean ratio) separated by 8 x 18 degrees of circular
arc (144 degrees) always passes through the circumference of the
inner circle (whose radius is equal to the lesser segment of the
extreme/ mean ratio) at two points which always subtend exactly
60 degrees of circular arc on that circle's circumference. The
chord of that arc, then, by virtue of the fact that things
equal to the same thing are equal to each other, is always
equal to the length of the radius of the inner circle and to the
length of the lesser segment of the extreme/ mean ratio. To repeat
the important fact here: this is always true when inner
and outer circle have radii equal to lesser and extreme segment,
when the circles are concentric, and when half the mean segment
is used to measure the 18 degree intervals of their respective
divisions into 20 equal parts. This is always true as well
without regard to the length of the initial given finite straight
line that is cut in extreme/ mean ratio. The following figure
illustrates this Maya "proof" of the equilateral triangle,
where the area shaded in red is that triangle:
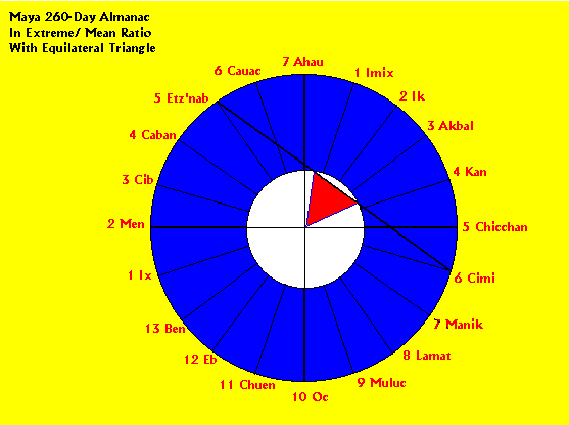
It is also true that the exposure of the equilateral triangle in this figure is a naturally occurring feature of its calendrical expression because there are only, and exactly, 13 numerical coefficients in the structure of the tzolkin. What this means is that there are always seven "empty" places on the intersection points between the 18 degree angle lines and the circumference of the inner circle when all thirteen numbers are deployed on consecutive spaces for the currently articulated day-names. That configuration in turn leaves 8 x 18 degree angles between the first and last numbers deployed in every sequence of thirteen consecutive days. Hence, every straight line connecting the first and last 18-degree angle mark which holds the first and last number always subtends a 60 degree arc on the inner circle. In other words, the equilateral triangle is always exposed by inference, at least, as each successive day of the tzolkin is counted. In the figure above, the number 6 (at 6 Cimi) and the number 5 (at 5 Etz'nab) are the first and last numbers and days in this sequence of 13 days. When the 6 is moved to its next position adjacent to Cauac, marking the day-name 6 Cauac, the line subtending the base of the equilateral triangle shifts to its next location between 6 Cauac and 7 Manik. This revolving structure of equilateral triangles delineated by the revolving straight line between first and last marked days as the count moves forward in the tzolkin is determined by the necessary conditions of the figure itself and cannot be termed coincidental to it. To suppose the Maya were unaware of this feature of their 260-day calendar seems disingenuous. To prove conclusively that they did know, however, will probably remain elusive.
As noted in the previous discussion of the figure, it was not drawn with a compass and a straight-edge for the purpose of this illustration and for that reason the configuration here is only meant to be approximate. Hence, and in order to verify the validity of the claim being put forward here, it is necessary to construct this figure using a compass and a straight-edge.
A final thought: since the line which cuts the 60 degree arc
on the inner circle always subtends 144 degrees of arc on the
outer circle, where 8 and 12 divisions of 18 degrees each falls
just short of the exact value of the extreme/ mean ratio (with
8 and 13 being the proper division at .6153846), it might be worthwhile
to contemplate the adjustment Maya astronomers made to accommodate
this shortfall when they fixed the length of their calendrical
Baktun interval at 144,000 days. Counting 13 Baktuns
in each Long Count notational system brings everything back to
its proper point of departure in comparing, as it were, degrees
in a circle (360) to days in a Tun (360).
Part II: The absence of binary opposition in calendrical harmonics.
An obvious fact based on simple definition is that opposition cannot be said to exist in any actual articulation of harmonic constructs. Harmony is the absence of opposition. In Classic period Maya conceptualizations of space and time, which are always integrated by virtue of the geometrical figure under scrutiny here, the idea that overrides the concept of binary opposition is the insertion of a mirror between one side of the figure and the other. In the example given above, a second straight line, which connects the points on the outer circle identified by 3 Cib and 8 Lamat, can be added to the figure to create the base-line of a second equilateral triangle whose apex is also located at the center of the two concentric circles. Since the second line (3 Cib to 8 Lamat) is parallel to the first line (between 5 Etz'nab and 6 Cimi), where both lines subtend opposite and equal values of 144 degrees on the same circumference of the outer circle, and where the line marked by 4 Caban and 7 Manik exactly bisects the opposite and equal 36 degree angles between 3 Cib and 5 Etz'nab, on one side of the figure, and between 6 Cimi and 8 Lamat, on the other, that line is also parallel to the two lines that subtend the equal and opposite base-lines of the two diametrically opposed equilateral triangles. Saying that the line between 4 Caban and 7 Manik represents a mirror in Classic period Maya conceptualizations of space and time is doing nothing more nor less than acknowledging what is only obvious from the figure itself. This is true because the two equilateral triangles occupy exactly the same space in the context of the two equal but opposite 72 degree angles marked between 7 Ahau and 4 Kan, on one side of the figure, and by 10 Oc and 1 Ix, on the other. What is equally apparent here is that the lesser angles, shaded in green, on one side of the equilateral triangles, and the greater angles, also shaded in green, on the other side, are exactly reversed in their locations relative the figure as a whole on opposite sides of the mirror represented by the 4 Caban and 7 Manik line. That reversal of location demonstrates what is meant by calling these two equilateral triangles mirror-images of each other. The following figure demonstrates these facts:

Also true here, of course, is that the lines drawn between 7 Ahau and 10 Oc and 5 Chicchan and 2 Men, the ones which quarter the two circles along their north-south and east-west axis lines, perform the same function as mirrors in the figure. The areas shaded in yellow are meant to illustrate this feature of the configuration. The point to be taken here is that every 18 degree angle line in the figure, from one diametrically opposed side of the circles to the other, always functions as a mirror reflecting opposite halves of the structure. Individual figures that appear in the structure by virtue of drawing straight lines through consistently opposed points always produce equal and opposite figures on the other side of the configuration. Since there is never any variation in terms of where diametrically opposed points are located relative to each other from one side of the mirror to the other, except to note that they are always mirror-images of each other relative to the whole, it becomes difficult, if not impossible, to quantify and qualify any significant differentiation between one diametrically opposed point or figure from its identical twin on the other side of the mirror. To say, then, that two points or figures in this structure are binary opposites (good/ evil, same/ other, here/ there, now/ then) ceases to express any significant distinguishing characteristics in either quantity or quality as those terms are usually understood in Western religious and philosophical ideology. This is true in harmonic figures because Good possesses precisely the same quantification and qualification possessed by its diametrically opposed, mirror-imaged twin, Evil. This same observation can be made for every other binary opposition conceived in an harmonic structure. Since there is no meaningful way to differentiate one thing from the other, across the replicating line of the mirror, there is no ground for assigning anything that exists to one classification or the other. Any such assignment becomes an arbitrary distinction based on prejudice, as opposed to fact, in the absence of any meaningful differentiation.